Calculating pressure loss in pipes and hoses

Online pressure loss calculator for pipes and hoses

When a metering pump is operated, the pumped medium is transported through a hose or pipe. This always results in a certain pressure loss, which affects the achievable flow rate and the maximum achievable back pressure of the pump.

The extent of this pressure loss depends significantly on several factors:

the volume flow
the viscosity and density of the liquid,
the length and inner diameter of the pipe,
as well as the internal roughness of the hose or pipe used.

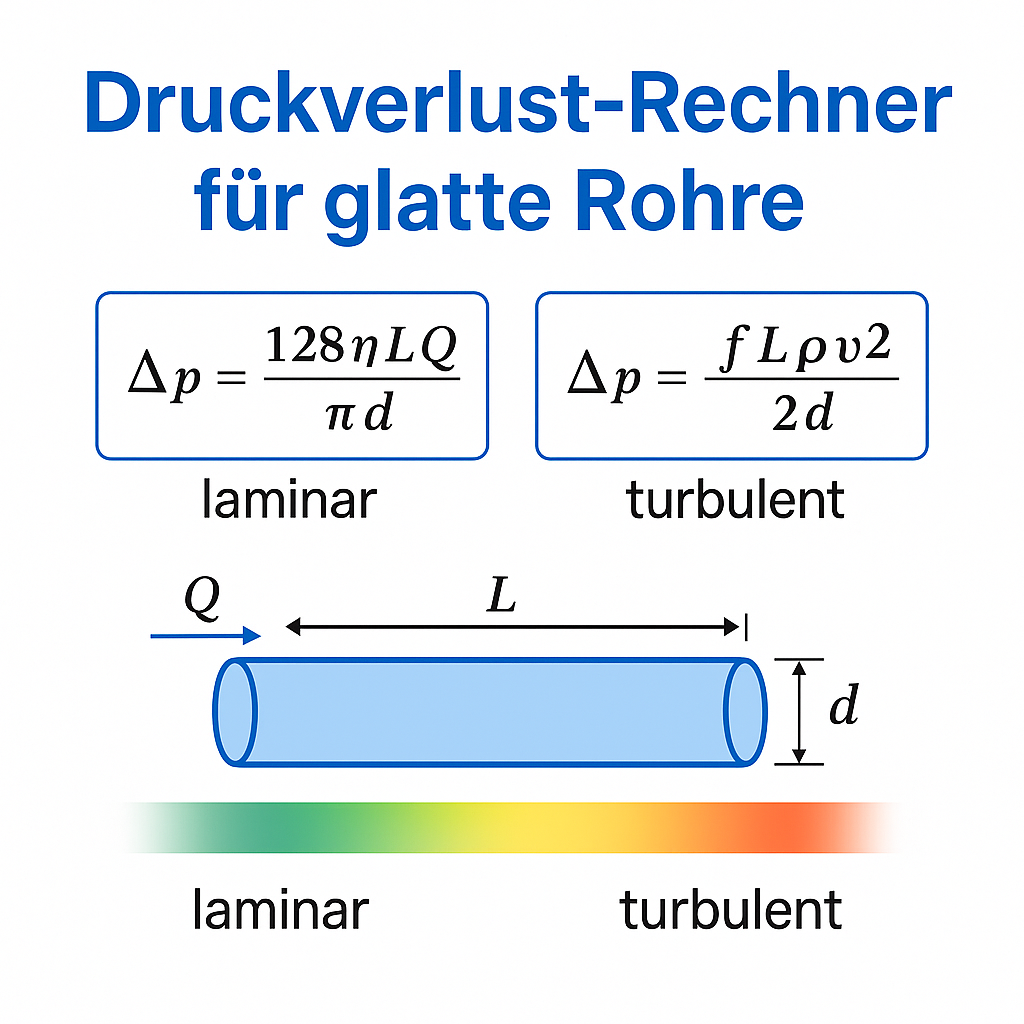
If the flow is laminar, the pressure loss can be calculated exactly using the Hagen-Poiseuille equation. However, turbulent flow occurs in many practical applications – especially at higher velocities, with small diameters, or with low-viscosity media. In these cases, the pressure loss is determined using the Darcy-Weisbach equation, where pipe roughness also plays a significant role.

The following calculator takes both models into account, automatically determines the Reynolds number and indicates which calculation is relevant for the selected application.


      
		   "
      

      
        
          Volume flow
          
            
            
          
        

        
          Pipe length (m)
          
        

        
          Pipe diameter (mm)
          
        

        
          Viscosity (mPa·s)
          
        

        
          Density (kg/m³)
          
        

        
          Internal roughness k (mm)
          
            
            
          
          
            Standard values, k in millimeters. Enter your own value for "User-defined".
          
        

        
          output value in

How do you calculate the pressure loss in a pipeline?

Pressure loss results from friction between the fluid and the pipe wall. Depending on the flow pattern, it is calculated either according to the Hagen-Poiseuille equation (laminar flow) or the Darcy-Weisbach equation (turbulent flow). The calculator on this page takes both models into account and indicates which calculation is relevant for your input.

When is a flow considered laminar or turbulent?

The flow pattern is determined by the Reynolds number (Re):

Re < 2.300 → laminar
Re 2.300–3.000 → Transition area
Re > 3.000 → turbulent

The computer automatically calculates the Reynolds number and displays the flow range in color.

Why do the two pressure loss formulas differ so much?

Because they apply to completely different flow regimes:

Hagen–Poiseuille → laminar, low speeds, highly viscous media, low Reynolds number
Darcy–Weisbach → turbulent, higher velocities, low-viscosity media, realistic pipe roughness

In turbulent flow, pressure losses are significantly higher, often by a factor of 10 or more.

What role does pipe roughness play?

The internal roughness (k) describes how smooth or rough a pipe or hose is. The rougher the material, the more the fluid is swirled – and the pressure loss increases. The calculator provides typical roughness values for:

PTFE tubing
Stainless steel pipes
PE/PVC hoses
steel pipes
and also allows user-defined values.

What does the Reynolds number mean in the context of metering pumps?

The Reynolds number is particularly important for metering pumps because small pipe diameters and high flow rates quickly lead to turbulent flow.
That means:
→ More pressure loss than expected
→ Higher load on the pump
→ Lower achievable flow rate

The calculator displays the Reynolds number so you can quickly assess whether a system is operating in the laminar-turbulent range.

How do temperature and viscosity affect pressure loss?

As the temperature increases, the viscosity of a liquid decreases. Lower viscosity → higher Reynolds number → flow becomes more turbulent → pressure drop increases. At high temperatures, the pressure drop can therefore be significantly greater than at room temperature.

Why does my pressure loss reading give different results than external websites?

Many online calculators use different assumptions, e.g.:

fixed pipe roughness
simplified friction coefficients
No difference between laminar/turbulent
general water values (20 °C)

The calculator on this page displays both models (laminar/turbulent) and uses realistic inputs, which is why the results are more transparent and precise.

How can I reduce the pressure loss in my application?

Typical measures include:

Choose a larger inner diameter.
shorter cable nutzen
smoother materials (e.g. PTFE instead of PE)
Avoid sharp curves
Viscosity can be influenced by temperature.

Even a small increase in diameter often has a dramatically reducing pressure loss.